| NCERT Exemplar Solutions | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
Chapter 5 Introduction To Euclid's Geometry
Welcome to this comprehensive resource offering detailed explanations and insightful answers for the NCERT Exemplar problems for Class 9 Mathematics, focusing on the foundational chapter: Introduction to Euclid's Geometry (Chapter 5). Unlike chapters centered on calculations or algebraic manipulation, the Exemplar questions in this area are designed to rigorously test and deepen students' conceptual understanding, cultivate logical reasoning abilities, and foster an appreciation for the axiomatic structure that underpins classical geometry, as established by Euclid over two millennia ago. The focus is less on "doing" geometry and more on "understanding the rules of the game."
The solutions provided here delve into the core elements of Euclid's approach as presented in his seminal work, "Elements." This begins with discussing Euclid's initial definitions for fundamental concepts like a point ("that which has no part"), a line ("breadthless length"), and a surface ("that which has length and breadth only"). The solutions acknowledge the inherent limitations and the essentially undefined nature of these starting terms, a key aspect of any formal system.
A crucial distinction emphasized in the solutions is between Axioms (also referred to as Common Notions) and Postulates. Axioms are presented as self-evident truths assumed to be applicable across all branches of reasoning (e.g., "Things which are equal to the same thing are equal to one another"). Postulates, on the other hand, are assumptions specific to geometry, required to begin geometric reasoning. Euclid's five postulates are central to this chapter, and the solutions explain each one clearly:
- Postulate 1: A straight line segment can be drawn joining any two points.
- Postulate 2: Any straight line segment can be extended indefinitely in a straight line.
- Postulate 3: A circle can be drawn with any center and any radius.
- Postulate 4: All right angles are equal to one another.
- Postulate 5 (Parallel Postulate): If a straight line falling on two straight lines makes the interior angles on the same side of it taken together less than two right angles, then the two straight lines, if produced indefinitely, meet on that side on which the sum of angles is less than two right angles.
The significance and implications of these postulates, particularly the historically debated fifth postulate, are discussed. The solutions also address the concept of equivalent versions of the fifth postulate, the most famous being Playfair's Axiom ("Through a given point not on a given line, exactly one parallel line can be drawn to the given line").
The Exemplar problems in this chapter are predominantly theoretical and reasoning-based. They often require students to:
- Correctly identify whether a given statement represents an axiom, a postulate, or a definition within Euclid's framework.
- Logically deduce simple geometric results directly from specific axioms or postulates (e.g., proving that two distinct lines cannot have more than one point in common, using the postulate about drawing a unique line between two points).
- Grasp the concept of consistency within an axiomatic system (the idea that the axioms and postulates should not lead to contradictions).
- Recognize and compare different but logically equivalent geometric statements, especially concerning parallel lines.
Addressing diverse question formats (MCQs testing definitions/implications, Fill-in-the-Blanks needing key terms, True/False assessing logical validity, Short/Long Answer demanding explanations/justifications), these solutions provide clear definitions, construct logical arguments rigorously justified by citing specific axioms or postulates, elucidate the pivotal role of the parallel postulate, and discuss the nature of undefined terms in mathematics. Engaging with this resource is crucial for developing foundational logical thinking skills, understanding the principles of deductive reasoning that form the basis of mathematical proof, and appreciating the historical evolution and enduring structure of Euclidean geometry.
Sample Question 1 to 6 (Before Exercise 5.1)
Write the correct answer:
Sample Question 1: Euclid’s second axiom (as per order given in the Textbook for Class IX) is
(A) The things which are equal to the same thing are equal to one another.
(B) If equals be added to equals, the wholes are equal.
(C) If equals be subtracted from equals, the remainders are equals.
(D) Things which coincide with one another are equal to one another.
Answer:
The correct answer is option (B).
According to the NCERT Class IX Textbook, Euclid's second axiom is:
If equals be added to equals, the wholes are equal.
Sample Question 2: Euclid’s fifth postulate is
(A) The whole is greater than the part.
(B) A circle may be described with any centre and any radius.
(C) All right angles are equal to one another.
(D) If a straight line falling on two straight lines makes the interior angles on the same side of it taken together less than two right angles, then the two straight lines if produced indefinitely, meet on that side on which the sum of angles is less than two right angles.
Answer:
The correct answer is option (D).
Euclid's fifth postulate states:
If a straight line falling on two straight lines makes the interior angles on the same side of it taken together less than two right angles, then the two straight lines if produced indefinitely, meet on that side on which the sum of angles is less than two right angles.
Sample Question 3: The things which are double of the same thing are
(A) equal
(B) unequal
(C) halves of the same thing
(D) double of the same thing
Answer:
The correct answer is option (A).
This can be understood using Euclid's axioms.
According to Euclid's first axiom:
Things which are equal to the same thing are equal to one another.
Let the same thing be represented by a quantity $x$.
Let the two things be $A$ and $B$.
If $A$ is double of $x$, then $A = 2x$.
If $B$ is double of $x$, then $B = 2x$.
Since both $A$ and $B$ are equal to $2x$ (the same thing), by Euclid's first axiom, $A$ must be equal to $B$.
Therefore, the things which are double of the same thing are equal.
Sample Question 4: Axioms are assumed
(A) universal truths in all branches of mathematics
(B) universal truths specific to geometry
(C) theorems
(D) definitions
Answer:
The correct answer is option (A).
Axioms are basic universal truths that are assumed without proof and are used throughout different branches of mathematics, not just geometry.
Postulates are similar to axioms but are considered to be specific to geometry.
Theorems are statements that are proved using definitions, axioms, previously proved theorems, and logical reasoning.
Definitions explain the meanings of terms.
Therefore, axioms are assumed universal truths in all branches of mathematics.
Sample Question 5: John is of the same age as Mohan. Ram is also of the same age as Mohan. State the Euclid’s axiom that illustrates the relative ages of John and Ram
(A) First Axiom
(B) Second Axiom
(C) Third Axiom
(D) Fourth Axiom
Answer:
The correct answer is option (A).
Let John's age be $J$, Mohan's age be $M$, and Ram's age be $R$.
Given that John is of the same age as Mohan, we have $J = M$.
Given that Ram is also of the same age as Mohan, we have $R = M$.
Since both $J$ and $R$ are equal to the same quantity $M$, according to Euclid's First Axiom, things which are equal to the same thing are equal to one another.
Therefore, $J = R$.
This illustrates Euclid's First Axiom.
Sample Question 6: If a straight line falling on two straight lines makes the interior angles on the same side of it, whose sum is 120°, then the two straight lines, if produced indefinitely, meet on the side on which the sum of angles is
(A) less than 120°
(B) greater than 120°
(C) is equal to 120°
(D) greater than 180°
Answer:
The correct answer is option (C).
This question is based on Euclid's Fifth Postulate.
Euclid's Fifth Postulate states: "If a straight line falling on two straight lines makes the interior angles on the same side of it taken together less than two right angles, then the two straight lines if produced indefinitely, meet on that side on which the sum of angles is less than two right angles."
Two right angles are equal to $2 \times 90^\circ = 180^\circ$.
In the given problem, the sum of the interior angles on one side is $120^\circ$.
Since $120^\circ < 180^\circ$, the condition mentioned in the postulate is satisfied.
According to the postulate, the two straight lines, if produced indefinitely, will meet on the side where the sum of the interior angles is less than two right angles.
The sum of the angles on that side is given as $120^\circ$.
Therefore, the lines will meet on the side where the sum of angles is $120^\circ$.
Exercise 5.1
Question 1. The three steps from solids to points are :
(A) Solids - surfaces - lines - points
(B) Solids - lines - surfaces - points
(C) Lines - points - surfaces - solids
(D) Lines - surfaces - points - solids
Answer:
A solid has three dimensions. Its boundaries are surfaces, which have two dimensions.
The boundaries of surfaces are lines, which have one dimension.
The boundaries of lines are points, which have no dimensions.
Therefore, the correct sequence from solids to points is Solids - surfaces - lines - points.
Thus, the correct option is (A).
Question 2. The number of dimensions, a solid has :
(A) 1
(B) 2
(C) 3
(D) 0
Answer:
In geometry, a solid is a three-dimensional figure.
It has length, width, and height, which are three dimensions.
Therefore, a solid has 3 dimensions.
The correct option is (C).
Question 3. The number of dimensions, a surface has :
(A) 1
(B) 2
(C) 3
(D) 0
Answer:
A surface is a geometric entity that has only two dimensions.
These dimensions can be thought of as length and width, or breadth. A surface has no thickness.
Therefore, a surface has 2 dimensions.
The correct option is (B).
Question 4. The number of dimension, a point has :
(A) 0
(B) 1
(C) 2
(D) 3
Answer:
In geometry, a point is a primitive notion that represents a specific location.
A point has no size, no length, no width, and no depth.
Therefore, a point has 0 dimensions.
The correct option is (A).
Question 5. Euclid divided his famous treatise “The Elements” into :
(A) 13 chapters
(B) 12 chapters
(C) 11 chapters
(D) 9 chapters
Answer:
Euclid's famous work, "The Elements", is a mathematical treatise consisting of 13 books (often referred to as chapters).
These books cover plane geometry, solid geometry, and number theory.
Therefore, Euclid divided his treatise into 13 chapters (books).
The correct option is (A).
Question 6. The total number of propositions in the Elements are :
(A) 465
(B) 460
(C) 13
(D) 55
Answer:
Euclid's Elements contains a vast number of geometric propositions and theorems.
The total number of propositions in Euclid's Elements is widely cited as 465.
These propositions are spread across the 13 books of the treatise.
Therefore, the correct number of propositions is 465.
The correct option is (A).
Question 7. Boundaries of solids are :
(A) surfaces
(B) curves
(C) lines
(D) points
Answer:
Analysis of the Question:
This question is based on the fundamental definitions of geometry as laid out by Euclid. It explores the relationship between geometric objects of different dimensions (solids, surfaces, lines, and points).
Euclidean Hierarchy:
Euclidean geometry defines a hierarchy of dimensions where an object of a certain dimension is bounded by objects of a lower dimension.
- A solid (3-dimensional) is bounded by surfaces (2-dimensional).
- A surface (2-dimensional) is bounded by lines (1-dimensional).
- A line (1-dimensional) is bounded by points (0-dimensional).
Explanation:
A solid is an object that has three dimensions: length, breadth, and depth. To define its extent or boundary, we need a two-dimensional entity. This boundary is a surface. The surface encloses the volume of the solid.
Example:
Consider a cuboid (like a box). It is a solid object. Its boundaries are its six rectangular faces. Each face is a two-dimensional surface. Similarly, the boundary of a sphere (a solid) is its single continuous curved surface.
Conclusion:
Following Euclid's definitions and the dimensional hierarchy, the boundaries of solids are surfaces.
The correct option is (A).
Question 8. Boundaries of surfaces are :
(A) surfaces
(B) curves
(C) lines
(D) points
Answer:
Analysis of the Question:
This question continues with the fundamental definitions of Euclidean geometry, asking about the boundaries of two-dimensional objects (surfaces).
Euclidean Hierarchy:
As established in the previous question, Euclidean geometry follows a dimensional hierarchy:
- A solid (3D) is bounded by surfaces (2D).
- A surface (2D) is bounded by lines (1D).
- A line (1D) is bounded by points (0D).
Explanation:
A surface is an object with two dimensions: length and breadth. According to Euclid's 6th definition, "The edges of a surface are lines." These lines define the extent of the surface. In this context, the term 'line' can refer to both straight lines and curves.
Example:
Consider a rectangular sheet of paper (a surface). Its boundaries are the four straight line segments that form its edges. A circular disc (a surface) is bounded by its circumference, which is a curved line.
Conclusion:
Following Euclid's definitions and the dimensional hierarchy, the boundaries of surfaces are lines.
The correct option is (C).
Question 9. In Indus Valley Civilisation (about 3000 B.C.), the bricks used for construction work were having dimensions in the ratio
(A) 1 : 3 : 4
(B) 4 : 2 : 1
(C) 4 : 4 : 1
(D) 4 : 3 : 2
Answer:
Archaeological findings from the Indus Valley Civilisation (also known as Harappan Civilisation) dating back to around 3000 B.C. show a remarkable consistency in the dimensions of baked bricks used for construction.
This standardization is one of the notable features of the civilization's urban planning.
The dimensions of the bricks were typically in the ratio of length : width : height which was consistently maintained as 4 : 2 : 1.
This specific ratio ensured structural stability and ease of construction.
Therefore, the dimensions of the bricks were in the ratio 4 : 2 : 1.
The correct option is (B).
Question 10. A pyramid is a solid figure, the base of which is
(A) only a triangle
(B) only a square
(C) only a rectangle
(D) any polygon
Answer:
A pyramid is a polyhedron formed by connecting a polygonal base and a point, called the apex.
The lateral faces of a pyramid are triangles that meet at the apex.
The shape of the base determines the type of pyramid. For example, a pyramid with a triangular base is called a triangular pyramid (or tetrahedron), a pyramid with a square base is a square pyramid, a pyramid with a pentagonal base is a pentagonal pyramid, and so on.
Thus, the base of a pyramid can be any polygon.
The correct option is (D).
Question 11. The side faces of a pyramid are :
(A) Triangles
(B) Squares
(C) Polygons
(D) Trapeziums
Answer:
A pyramid is a solid figure formed by a polygonal base and triangular faces that meet at a common point called the apex.
The faces that connect the base to the apex are the side faces (or lateral faces) of the pyramid.
By definition, these side faces are always Triangles, regardless of the shape of the polygonal base.
For example, a square pyramid has a square base and four triangular side faces. A triangular pyramid has a triangular base and three triangular side faces.
Therefore, the side faces of a pyramid are Triangles.
The correct option is (A).
Question 12. It is known that if x + y = 10 then x + y + z = 10 + z. The Euclid’s axiom that illustrates this statement is :
(A) First Axiom
(B) Second Axiom
(C) Third Axiom
(D) Fourth Axiom
Answer:
The given statement is: If $x + y = 10$, then $x + y + z = 10 + z$.
This statement shows that if we have two quantities that are equal ($x+y$ and $10$), and we add the same quantity ($z$) to both of them, the resulting quantities ($x+y+z$ and $10+z$) remain equal.
Let's recall Euclid's axioms (also known as common notions).
One of Euclid's axioms directly addresses this situation.
Euclid's Second Axiom states: "If equals be added to equals, the wholes are equal."
In the given statement, "$x+y$" and "$10$" are the initial "equals". When "$z$" (an "equal" quantity being added to both) is added to both sides of the equality $x+y = 10$, the result is $x+y+z = 10+z$, which are the "wholes" that are equal.
Thus, the statement $x+y=10 \implies x+y+z=10+z$ is an illustration of Euclid's Second Axiom.
The correct option is (B).
Question 13. In ancient India, the shapes of altars used for house hold rituals were :
(A) Squares and circles
(B) Triangles and rectangles
(C) Trapeziums and pyramids
(D) Rectangles and squares
Answer:
In ancient India, particularly during the Vedic period (as documented in the Sulba Sutras), geometric principles were applied to the construction of altars (vedis) for religious rituals.
These altars had specific shapes and sizes, often representing symbolic meanings.
For household rituals, the common shapes prescribed for altars were squares and circles.
More complex shapes like trapeziums and bird shapes were used for larger public or royal rituals, but squares and circles were fundamental shapes for household ceremonies.
Therefore, the shapes of altars used for household rituals in ancient India were Squares and circles.
The correct option is (A).
Question 14. The number of interwoven isosceles triangles in Sriyantra (in the Atharvaveda) is:
(A) Seven
(B) Eight
(C) Nine
(D) Eleven
Answer:
The Sriyantra (also known as Shri Chakra) is a sacred geometric diagram consisting of interwoven triangles.
This diagram is a central element in the worship of the goddess Tripura Sundari in Hindu tradition and is mentioned in various texts, including parts related to Vedic practices.
The core structure of the Sriyantra is formed by nine interwoven isosceles triangles.
Of these nine, four triangles point upwards, representing Shiva (the masculine principle), and five point downwards, representing Shakti (the feminine principle). The intersection of these nine triangles creates a total of 43 smaller triangles within the yantra.
Therefore, the number of interwoven isosceles triangles in the Sriyantra is Nine.
The correct option is (C).
Question 15. Greek’s emphasised on :
(A) Inductive reasoning
(B) Deductive reasoning
(C) Both A and B
(D) Practical use of geometry
Answer:
The ancient Greeks, particularly figures like Euclid, are renowned for establishing geometry as a systematic and logical science.
They developed a system where geometric theorems were derived from a set of basic assumptions (axioms and postulates) through rigorous logical steps.
This method of reasoning, where conclusions are reached by applying general principles to specific cases, is known as deductive reasoning.
While other civilizations used geometry for practical purposes (like construction and surveying) and might have used inductive reasoning to discover geometric properties, the Greeks' significant contribution was the emphasis on and formalization of deductive reasoning in geometry.
Therefore, the Greeks primarily emphasised Deductive reasoning.
The correct option is (B).
Question 16. In Ancient India, Altars with combination of shapes like rectangles, triangles and trapeziums were used for :
(A) Public worship
(B) Household rituals
(C) Both A and B
(D) None of A, B, C
Answer:
In ancient India, particularly as described in the Sulba Sutras, the construction of sacrificial altars (vedis) involved precise geometry and various shapes.
Simple altars for household rituals were typically squares or circles (as discussed in Question 13).
More elaborate altars, often involving combinations of shapes like rectangles, triangles, and trapeziums, were constructed for larger and more significant rituals.
These complex altars, such as those shaped like birds (e.g., the Falcon Altar, Śyenaciti), required detailed geometric calculations and constructions using these combined shapes. They were typically used for major sacrifices and rituals performed by the community or rulers, which fall under the category of public worship.
Therefore, altars with combinations of shapes like rectangles, triangles, and trapeziums were used for Public worship.
The correct option is (A).
Question 17. Euclid belongs to the country :
(A) Babylonia
(B) Egypt
(C) Greece
(D) India
Answer:
Euclid was an ancient Greek mathematician, often referred to as the "father of geometry".
He was active in Alexandria, Egypt, during the reign of Ptolemy I (323–283 BC). Although he lived and worked in Alexandria, which was a major intellectual center of the Hellenistic world, he was of Greek origin and heritage. Alexandria itself was founded by Alexander the Great and was a center of Greek culture.
His work heavily influenced the development of Western mathematics for over two thousand years.
Therefore, Euclid belongs to the country Greece.
The correct option is (C).
Question 18. Thales belongs to the country :
(A) Babylonia
(B) Egypt
(C) Greece
(D) Rome
Answer:
Thales of Miletus was an ancient Greek philosopher, mathematician, and astronomer.
He lived in Miletus, an ancient Greek city on the western coast of Asia Minor (present-day Turkey). Although Miletus is now in Turkey, it was part of the ancient Greek world and culture.
He is often credited as the first individual in Western civilization to apply deductive reasoning to geometry and is considered one of the founders of Greek philosophy.
Therefore, Thales belongs to Greece.
The correct option is (C).
Question 19. Pythagoras was a student of :
(A) Thales
(B) Euclid
(C) Both A and B
(D) Archimedes
Answer:
Pythagoras was an ancient Greek philosopher and mathematician, famous for the Pythagorean theorem.
Historical accounts and traditions suggest that Pythagoras traveled extensively and was influenced by various scholars.
Several historical sources indicate that Pythagoras studied under Thales, who was an older and well-respected philosopher and mathematician in the Greek world. Thales is said to have encouraged Pythagoras to travel to Egypt to further his studies.
Euclid and Archimedes lived after Pythagoras. Euclid lived around 300 BC, while Pythagoras lived around 570–495 BC. Archimedes lived even later, around 287–212 BC. Therefore, Pythagoras could not have been a student of Euclid or Archimedes.
Thus, Pythagoras was a student of Thales.
The correct option is (A).
Question 20. Which of the following needs a proof ?
(A) Theorem
(B) Axiom
(C) Definition
(D) Postulate
Answer:
Let's consider the definitions of the given terms in a geometric system:
Definition: A statement that explains the meaning of a geometric term or concept. Definitions are agreed upon and do not require proof.
Axiom (or Common Notion): A fundamental truth or statement that is accepted as true without proof. It is considered self-evident.
Postulate: Similar to an axiom, a postulate is a statement that is accepted as true without proof, often specific to geometry.
Theorem: A statement that can be proven to be true using logical reasoning based on definitions, axioms, postulates, and previously proven theorems.
Based on these definitions, the term that requires a proof is a Theorem.
The correct option is (A).
Question 21. Euclid stated that all right angles are equal to each other in the form of
(A) an axiom
(B) a definition
(C) a postulate
(D) a proof
Answer:
Euclid's Elements is built upon a set of basic assumptions that are accepted without proof. These assumptions are categorized as Definitions, Axioms (or Common Notions), and Postulates.
Axioms are general truths that apply across mathematics, while Postulates are fundamental assumptions specific to geometry.
The statement that "all right angles are equal to each other" is a fundamental geometric assumption necessary for building Euclidean geometry.
In Euclid's system, this statement is specifically listed as the fourth postulate (Postulate 4).
Therefore, Euclid stated that all right angles are equal to each other in the form of a postulate.
The correct option is (C).
Question 22. ‘Lines are parallel if they do not intersect’ is stated in the form of
(A) an axiom
(B) a definition
(C) a postulate
(D) a proof
Answer:
In Euclidean geometry, fundamental terms are introduced through definitions, axioms, and postulates.
A definition provides the meaning of a term.
An axiom or postulate is a basic assumption accepted without proof.
A proof is a logical argument used to establish the truth of a theorem.
The statement "Lines are parallel if they do not intersect" precisely defines what parallel lines are. It gives the characteristic property that distinguishes parallel lines from intersecting lines.
This is the standard definition of parallel lines in Euclidean geometry. Although related to Euclid's Fifth Postulate, the statement itself is a definition.
Therefore, the statement is in the form of a definition.
The correct option is (B).
Sample Question 1 (Before Exercise 5.2)
Sample Question 1: Write whether the following statements are True or False?
Justify your answer
(i) Pyramid is a solid figure, the base of which is a triangle or square or some other polygon and its side faces are equilateral triangles that converges to a point at the top.
(ii) In Vedic period, squares and circular shaped altars were used for household rituals, while altars whose shapes were combination of rectangles, triangles and trapeziums were used for public worship.
(iii) In geometry, we take a point, a line and a plane as undefined terms.
(iv) If the area of a triangle equals the area of a rectangle and the area of the rectangle equals that of a square, then the area of the triangle also equals the area of the square.
(v) Euclid’s fourth axiom says that everything equals itself.
(vi) The Euclidean geometry is valid only for figures in the plane.
Answer:
(i) Statement: Pyramid is a solid figure, the base of which is a triangle or square or some other polygon and its side faces are equilateral triangles that converges to a point at the top.
Conclusion: False
Justification: The definition of a pyramid is mostly correct, but the assertion that its side faces are equilateral triangles is not always true. The side faces of a pyramid are indeed triangles that meet at a common vertex (the apex). However, they are only equilateral in specific cases (like a regular tetrahedron). For a right pyramid with a regular polygon as its base, the side faces are congruent isosceles triangles. For an oblique pyramid, the side faces can even be scalene triangles.
(ii) Statement: In Vedic period, squares and circular shaped altars were used for household rituals, while altars whose shapes were combination of rectangles, triangles and trapeziums were used for public worship.
Conclusion: True
Justification: This statement is historically accurate. The ancient Indian mathematical texts known as the Sulbasutras describe the construction of altars (Vedis). For household rituals, simpler shapes like squares and circles were prescribed. For large-scale public worship, more complex altars were constructed, often in the shape of a trapezium or a combination of rectangles, triangles, and trapeziums, with very specific area requirements.
(iii) Statement: In geometry, we take a point, a line and a plane as undefined terms.
Conclusion: True
Justification: In modern axiomatic systems of geometry, terms like 'point', 'line', and 'plane' are considered fundamental or "undefined" terms. While Euclid attempted to define them (e.g., "A point is that which has no part"), these are now seen as intuitive descriptions rather than rigorous definitions. The properties and relationships of these terms are established through a set of axioms or postulates, which are accepted without proof.
(iv) Statement: If the area of a triangle equals the area of a rectangle and the area of the rectangle equals that of a square, then the area of the triangle also equals the area of the square.
Conclusion: True
Justification: This statement is a direct application of Euclid's first axiom: "Things which are equal to the same thing are also equal to one another." Let A(triangle), A(rectangle), and A(square) be the respective areas. We are given A(triangle) = A(rectangle) and A(square) = A(rectangle). Since the area of the triangle and the area of the square are both equal to the same quantity (the area of the rectangle), they must be equal to each other. This is also known as the transitive property of equality.
(v) Statement: Euclid’s fourth axiom says that everything equals itself.
Conclusion: False
Justification: Euclid's fourth axiom states, "Things which coincide with one another are equal to one another." This is related to the idea of proving congruence by superposition. The statement "everything equals itself" is known as the reflexive property of equality, which is a more modern and fundamental concept not explicitly listed as one of Euclid's axioms.
(vi) Statement: The Euclidean geometry is valid only for figures in the plane.
Conclusion: False
Justification: Euclidean geometry is not limited to two-dimensional figures in a plane. It also includes solid geometry, which deals with three-dimensional objects like cubes, spheres, and pyramids in three-dimensional space. The axioms and postulates of Euclid apply to a "flat" space (a space with zero curvature), which can be two-dimensional (a plane) or three-dimensional.
Exercise 5.2
Write whether the following statements are True or False? Justify your answer :
Question 1. Euclidean geometry is valid only for curved surfaces.
Answer:
False
Justification: Euclidean geometry is based on Euclid's axioms and postulates, which describe properties of points, lines, and planes. It is the geometry of flat space. Euclidean geometry is valid for figures in a plane (a flat surface) and extends to three-dimensional space, but it is not valid for curved surfaces like the surface of a sphere. Geometry on curved surfaces is described by non-Euclidean geometries.
Question 2. The boundaries of the solids are curves.
Answer:
False
Justification: According to Euclid's definitions, the boundaries of solids are surfaces, not curves. For example, the boundary of a cube is made up of flat surfaces (squares), and the boundary of a sphere is a curved surface. While surfaces can have curved boundaries (lines), the boundary of a solid itself is a surface.
Question 3. The edges of a surface are curves.
Answer:
False
Justification: According to Euclid's definitions, the boundaries of surfaces are lines, not curves. A line is defined as "breadthless length". Lines can be straight or curved. The "edges" or boundaries of a surface can be straight lines (as in a square) or curved lines (as in a circle). Therefore, saying they are *only* curves is incorrect. The more accurate term for the boundary of a surface is a line, which can be straight or curved.
Question 4. The things which are double of the same thing are equal to one another.
Answer:
True
Justification: This statement is an application of Euclid's Axioms (Common Notions). Specifically, it relates to the idea of multiplying equals by the same quantity. If you have a quantity $x$, and you double it, you get $2x$. If you have another quantity $y$, and you double it, you get $2y$. If the original quantities were equal, i.e., $x = y$, then doubling both sides gives $2x = 2y$. This is implicitly covered by Euclid's common notion that "If equals be multiplied by equals, the wholes are equal" or can be seen as an extension of "things which are equal to the same thing are equal to one another" applied to doubling. It can also be directly derived from the axiom that "If equals be added to equals, the wholes are equal" by adding $x$ to $x$ and $y$ to $y$.
Let the "same thing" be represented by a quantity $k$.
Let the two "things" be $A$ and $B$.
The statement says that $A$ is double of $k$, so $A = 2k$.
The statement also says that $B$ is double of the same thing $k$, so $B = 2k$.
Since both $A$ and $B$ are equal to $2k$, by Euclid's First Axiom ("Things which are equal to the same thing are equal to one another"), we have $A = B$.
Alternatively, let $x$ and $y$ be two things which are double of the same thing, say $z$.
So, $x = 2z$ and $y = 2z$.
$x = 2z$
... (i)
$y = 2z$
... (ii)
From (i) and (ii), by Euclid's First Axiom, things which are equal to the same thing ($2z$) are equal to one another.
Thus, $x = y$.
The statement is consistent with Euclidean axioms.
Question 5. If a quantity B is a part of another quantity A, then A can be written as the sum of B and some third quantity C.
Answer:
True
Justification: This statement is consistent with Euclidean geometry and the fundamental understanding of quantities. If a quantity B is a part of a quantity A, it means that A is composed of B and whatever remains when B is removed from A. Let the remaining quantity be C. Then, the original quantity A is the sum of its part B and the remaining part C. This can be represented as $A = B + C$.
This concept is related to Euclid's Fifth Common Notion, which states that "the whole is greater than the part." This implies that if B is a proper part of A, then A contains B and something more (C, where C > 0). If B is the entire quantity A (meaning B is a part, albeit not a proper part), then C would be 0, and the statement $A = B + 0$ is still true.
Question 6. The statements that are proved are called axioms.
Answer:
False
Justification: In a logical system like Euclidean geometry, axioms are fundamental statements that are assumed to be true without proof. They are the starting points of the system. The statements that are proved using axioms, postulates, and logical reasoning are called theorems.
Question 7. “For every line l and for every point P not lying on a given line l, there exists a unique line m passing through P and parallel to l ” is known as Playfair’s axiom.
Answer:
True
Justification: The statement "For every line $l$ and for every point P not lying on a given line $l$, there exists a unique line $m$ passing through P and parallel to $l$" is indeed a common and equivalent formulation of Euclid's Fifth Postulate. This specific formulation is known as Playfair's Axiom, named after the Scottish mathematician John Playfair, who published it in 1795.
Question 8. Two distinct intersecting lines cannot be parallel to the same line.
Answer:
True
Justification: This statement is a direct consequence of Playfair's Axiom, which is equivalent to Euclid's Fifth Postulate. Playfair's Axiom states that through a point not on a given line, there is exactly one line parallel to the given line.
Let's assume, for the sake of contradiction, that two distinct intersecting lines, say line $p$ and line $q$, are both parallel to the same line $l$.
Since lines $p$ and $q$ are distinct and intersecting, they meet at a unique point, say P.
So, we have a point P, and a line $l$. Both line $p$ and line $q$ pass through P.
We assumed that line $p$ is parallel to line $l$, and line $q$ is also parallel to line $l$.
This means we have two distinct lines ($p$ and $q$) passing through the same point P that are both parallel to the same line $l$.
However, Playfair's Axiom says that through a point not on a given line, there exists a unique line parallel to the given line. Since P is the intersection point of $p$ and $q$, P cannot lie on line $l$ (because if it did, then $p$ and $q$ would intersect $l$ at P, contradicting that they are parallel to $l$).
The existence of two distinct lines ($p$ and $q$) passing through P and parallel to $l$ contradicts the uniqueness guaranteed by Playfair's Axiom.
Therefore, our initial assumption that two distinct intersecting lines can be parallel to the same line must be false.
Hence, two distinct intersecting lines cannot be parallel to the same line.
Question 9. Attempts to prove Euclid’s fifth postulate using the other postulates and axioms led to the discovery of several other geometries.
Answer:
True
Justification: For centuries after Euclid, mathematicians attempted to prove the Fifth Postulate from the first four axioms and postulates, believing it was not as self-evident as the others. These attempts were unsuccessful.
Eventually, in the 19th century, mathematicians like Lobachevsky, Bolyai, and Riemann explored what would happen if they assumed the negation of the Fifth Postulate while keeping the other Euclidean postulates.
Assuming different alternatives to the Fifth Postulate led to the development of consistent alternative geometric systems, known as non-Euclidean geometries (e.g., hyperbolic geometry, elliptic geometry). These geometries are valid mathematical systems but describe space differently than Euclidean geometry.
Thus, the attempts to prove Euclid's Fifth Postulate indeed led to the discovery of these other geometries.
Sample Question 1 to 4 (Before Exercise 5.3)
Sample Question 1: Ram and Ravi have the same weight. If they each gain weight by 2 kg, how will their new weights be compared ?
Answer:
Let the initial weight of Ram be $W_{\text{Ram}}$ and the initial weight of Ravi be $W_{\text{Ravi}}$.
Given that Ram and Ravi have the same weight, we can write:
$W_{\text{Ram}} = W_{\text{Ravi}}$
Each of them gains weight by 2 kg.
Ram's new weight will be $W_{\text{Ram}} + 2$.
Ravi's new weight will be $W_{\text{Ravi}} + 2$.
We need to compare their new weights, which are $W_{\text{Ram}} + 2$ and $W_{\text{Ravi}} + 2$.
We know that $W_{\text{Ram}}$ and $W_{\text{Ravi}}$ are equal quantities. We are adding the same quantity, 2 kg, to both of these equal quantities.
According to Euclid’s Second Axiom (Common Notion 2), "If equals be added to equals, the wholes are equal."
Applying this axiom, since $W_{\text{Ram}} = W_{\text{Ravi}}$, it follows that:
$W_{\text{Ram}} + 2 = W_{\text{Ravi}} + 2$
Therefore, their new weights will be equal.
Sample Question 2: Solve the equation a – 15 = 25 and state which axiom do you use here.
Answer:
The given equation is:
$a - 15 = 25$
To solve for $a$, we need to eliminate the $-15$ on the left side of the equation. We can do this by adding $15$ to both sides of the equation.
Adding 15 to both sides:
$(a - 15) + 15 = 25 + 15$
This simplifies to:
$a = 40$
The axiom used here is Euclid’s Second Axiom (Common Notion 2), which states:
"If equals be added to equals, the wholes are equal."
In this equation, we have the initial equality $a - 15 = 25$. We are adding the same quantity ($15$) to both equal sides ($a-15$ and $25$). The resulting sums ($a$ and $40$) are therefore equal.
Sample Question 3: In the Fig. 5.1, if ∠1 = ∠3, ∠2 = ∠4 and ∠3 = ∠4, write the relation between ∠1 and ∠2, using an Euclid’s axiom.

Answer:
Given:
$\angle 1 = \angle 3$
$\angle 2 = \angle 4$
$\angle 3 = \angle 4$
We have $\angle 1 = \angle 3$ and $\angle 3 = \angle 4$.
According to Euclid's First Axiom (Common Notion 1), "Things which are equal to the same thing are equal to one another."
Applying this axiom to the equalities $\angle 1 = \angle 3$ and $\angle 3 = \angle 4$, we can conclude that:
$\angle 1 = \angle 4$
Now we have $\angle 1 = \angle 4$ and it is also given that $\angle 2 = \angle 4$.
Again, applying Euclid's First Axiom, since both $\angle 1$ and $\angle 2$ are equal to the same thing ($\angle 4$), they must be equal to one another.
Therefore, the relation between $\angle 1$ and $\angle 2$ is:
$\angle 1 = \angle 2$
Sample Question 4: In Fig. 5.2, we have : AC = XD, C is the mid-point of AB and D is the mid-point of XY. Using an Euclid’s axiom, show that AB = XY

Answer:
Given:
$AC = XD$
C is the mid-point of AB
D is the mid-point of XY
Since C is the mid-point of AB, the length of the segment AB is twice the length of AC.
Thus, $AB = 2 \times AC$.
Similarly, since D is the mid-point of XY, the length of the segment XY is twice the length of XD.
Thus, $XY = 2 \times XD$.
We are given that $AC = XD$.
According to a Euclidean axiom (often stated as a common notion or derived property), "Doubles of equals are equal".
Since $AC$ and $XD$ are equal quantities, multiplying both by 2 results in equal quantities.
So, $2 \times AC = 2 \times XD$.
By substitution (since $AB = 2 \times AC$ and $XY = 2 \times XD$), we can conclude that:
$AB = XY$.
Exercise 5.3
Solve each of the following question using appropriate Euclid’s axiom:
Question 1. Two salesmen make equal sales during the month of August. In September, each salesman doubles his sale of the month of August. Compare their sales in September.
Answer:
Let the sales of the first salesman in August be $S_1$ and the sales of the second salesman in August be $S_2$.
According to the problem, their sales in August are equal:
$S_1 = S_2$
In September, each salesman doubles their sale of August.
The new sales for the first salesman in September ($S'_1$) will be $2 \times S_1$.
The new sales for the second salesman in September ($S'_2$) will be $2 \times S_2$.
We need to compare $S'_1$ and $S'_2$.
We know that $S_1 = S_2$. We are multiplying both sides of this equality by the same number, 2.
According to a Euclidean axiom (a consequence of Euclid's Second Axiom), "Doubles of equals are equal". This means if two quantities are equal, then multiplying both by 2 will result in quantities that are also equal.
Applying this, since $S_1 = S_2$, then $2 \times S_1 = 2 \times S_2$.
By substitution, we have $S'_1 = S'_2$.
Therefore, their sales in September will be equal.
Question 2. It is known that x + y = 10 and that x = z. Show that z + y = 10?
Answer:
Given:
$x + y = 10$
$x = z$
To Show:
$z + y = 10$
Solution:
We are given the equation:
$x + y = 10$
We are also given that:
$x = z$
According to Euclid’s First Axiom (Common Notion 1), "Things which are equal to the same thing are equal to one another." This axiom implies that if two quantities are equal, one can be substituted for the other in any mathematical statement without changing its truth.
Since $x$ is equal to $z$, we can substitute $z$ in place of $x$ in the equation $x + y = 10$.
Substituting $z$ for $x$, the equation becomes:
$z + y = 10$
This is what we were required to show.
Question 3. Look at the Fig. 5.3. Show that length AH > sum of lengths of AB + BC + CD.

Answer:
From the figure, we can observe that the line segment AH is composed of several smaller segments placed consecutively along the same straight line.
The length of the segment AH is the sum of the lengths of the segments AB, BC, CD, DE, EF, FG, and GH.
So, $AH = AB + BC + CD + DE + EF + FG + GH$.
The sum of the lengths of AB, BC, and CD is $AB + BC + CD$.
We can rewrite the equation for AH as:
$AH = (AB + BC + CD) + (DE + EF + FG + GH)$
Let the sum of lengths of AB + BC + CD be denoted as Quantity 1.
Let the sum of lengths of DE + EF + FG + GH be denoted as Quantity 2.
So, $AH = \text{Quantity 1} + \text{Quantity 2}$.
From the figure, it is clear that DE, EF, FG, and GH are positive lengths, so Quantity 2 = $DE + EF + FG + GH$ must be greater than zero.
$\text{Quantity 2} > 0$.
According to Euclid's Fifth Axiom (Common Notion 5), "The whole is greater than the part."
In this case, AH represents the "whole" length, and the sum of lengths AB + BC + CD represents a "part" of the whole length AH. Specifically, $AB + BC + CD$ is a part of AH, as AH also includes the lengths $DE + EF + FG + GH$.
Since $AB + BC + CD$ is a part of AH (and Quantity 2 $> 0$), the whole AH must be greater than this part.
Therefore, $AH > AB + BC + CD$.
Alternatively, since $AH = (AB + BC + CD) \ $$ + (DE + EF + FG + GH)$ and $DE + EF + FG + GH > 0$, adding a positive quantity $(DE + EF + FG + GH)$ to $(AB + BC + CD)$ results in a larger quantity (AH). This is an application of the axiom that if equals are added to unequals, the wholes are unequal. Or simply, adding a positive value increases the sum.
We have $AH - (AB + BC + CD) = DE + EF + FG + GH$.
Since $DE + EF + FG + GH > 0$, it follows that $AH - (AB + BC + CD) > 0$.
Adding $(AB + BC + CD)$ to both sides of the inequality:
$AH > AB + BC + CD$.
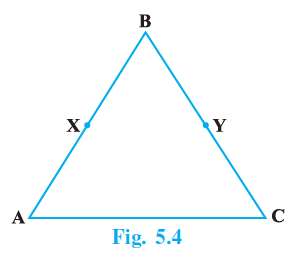
Question 4. In the Fig.5.4, we have AB = BC, BX = BY. Show that AX = CY
Answer:
Given:
$AB = BC$
$BX = BY$
To Show:
$AX = CY$
Solution:
From the figure, we can express the length of segment AB as the sum of the lengths of segments AX and BX:
$AB = AX + BX$
Similarly, we can express the length of segment BC as the sum of the lengths of segments BY and CY:
$BC = BY + CY$
We are given that $AB = BC$.
Substituting the expressions for AB and BC into the given equality, we get:
$AX + BX = BY + CY$
We are also given that $BX = BY$.
We have the equality $AX + BX = BY + CY$. We also know that the quantity $BX$ is equal to the quantity $BY$.
According to Euclid’s Third Axiom (Common Notion 3), "If equals be subtracted from equals, the remainders are equal."
We can subtract the equal quantities $BX$ from the left side and $BY$ from the right side of the equation $AX + BX = BY + CY$.
$(AX + BX) - BX = (BY + CY) - BY$
Simplifying both sides, we get:
$AX = CY$
Thus, we have shown that $AX = CY$ using Euclid's Third Axiom.
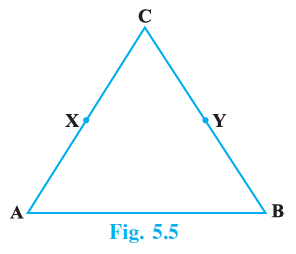
Question 5. In the Fig.5.5, we have X and Y are the mid-points of AC and BC and AX = CY. Show that AC = BC
Answer:
Given:
X is the mid-point of AC.
Y is the mid-point of BC.
$AX = CY$.
To Show:
$AC = BC$.
Solution:
Since X is the mid-point of the line segment AC, the length of AC is twice the length of AX.
$AC = 2 \times AX$
Since Y is the mid-point of the line segment BC, the length of BC is twice the length of BY. Also, $CY = BY$, and $BC = CY + BY = CY + CY = 2 \times CY$.
$BC = 2 \times CY$
We are given that $AX = CY$.
According to a Euclidean axiom, "Doubles of equals are equal". This means that if two quantities are equal, then multiplying both by the same number results in quantities that are also equal. This is related to Euclid's Second Axiom.
Since $AX$ and $CY$ are equal quantities, doubling both sides of the equality $AX = CY$ gives us:
$2 \times AX = 2 \times CY$
We know that $AC = 2 \times AX$ and $BC = 2 \times CY$.
Substituting $AC$ for $2 \times AX$ and $BC$ for $2 \times CY$ in the equation $2 \times AX = 2 \times CY$, we get:
$AC = BC$
Thus, we have shown that $AC = BC$. The axiom used is that doubles of equals are equal.
Question 6. In the Fig.5.6, we have

BX = $\frac{1}{2}$ AB
BY = $\frac{1}{2}$ BC and AB = BC.
Show that BX = BY
Answer:
Given:
$BX = \frac{1}{2} AB$
$BY = \frac{1}{2} BC$
$AB = BC$
To Show:
$BX = BY$
Solution:
We are given the relationship between BX and AB:
BX = $\frac{1}{2}$ AB
... (i)
We are also given the relationship between BY and BC:
BY = $\frac{1}{2}$ BC
... (ii)
And we are given that AB and BC are equal:
AB = BC
... (iii)
According to Euclid's Sixth Axiom (Common Notion 6), "Things which are halves of the same things are equal to one another." This axiom can also be interpreted as "halves of equals are equal".
From equation (iii), we know that AB and BC are equal quantities.
From equations (i) and (ii), BX is half of AB, and BY is half of BC.
Since AB and BC are equal, their halves must also be equal, according to Euclid's Sixth Axiom.
Therefore, $BX = BY$.
Alternatively, we can use substitution based on Euclid's First Axiom ("Things which are equal to the same thing are equal to one another").
From (iii), $AB = BC$.
Multiply both sides by $\frac{1}{2}$:
$\frac{1}{2} AB = \frac{1}{2} BC$
From (i), we know $BX = \frac{1}{2} AB$.
From (ii), we know $BY = \frac{1}{2} BC$.
Since both $BX$ and $BY$ are equal to the same quantity ($\frac{1}{2} AB$ which is equal to $\frac{1}{2} BC$), by Euclid's First Axiom, they are equal to each other.
Thus, $BX = BY$.
Question 7. In the Fig.5.7, we have ∠1 = ∠2, ∠2 = ∠3. Show that ∠1 = ∠3.

Answer:
Given:
$\angle 1 = \angle 2$
$\angle 2 = \angle 3$
To Show:
$\angle 1 = \angle 3$
Solution:
We are given two equalities:
$\angle 1 = \angle 2$
... (i)
$\angle 2 = \angle 3$
... (ii)
We can see that both $\angle 1$ and $\angle 3$ are equal to the same quantity, $\angle 2$.
According to Euclid’s First Axiom (Common Notion 1), "Things which are equal to the same thing are equal to one another."
Applying this axiom to the given equalities, since $\angle 1$ is equal to $\angle 2$ and $\angle 3$ is also equal to $\angle 2$, it follows that $\angle 1$ must be equal to $\angle 3$.
Therefore, $\angle 1 = \angle 3$.
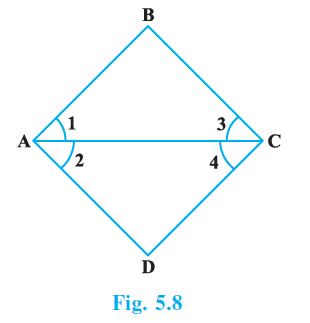
Question 8. In the Fig. 5.8, we have ∠1 = ∠3 and ∠2 = ∠4. Show that ∠A = ∠C
Answer:
Given:
$\angle 1 = \angle 3$
$\angle 2 = \angle 4$
To Show:
$\angle A = \angle C$
Solution:
From the figure, we can see that $\angle A$ is the sum of $\angle 1$ and $\angle 2$.
$\angle A = \angle 1 + \angle 2$
Similarly, $\angle C$ is the sum of $\angle 3$ and $\angle 4$.
$\angle C = \angle 3 + \angle 4$
We are given that $\angle 1 = \angle 3$ and $\angle 2 = \angle 4$.
We have two pairs of equal quantities: ($\angle 1$ and $\angle 3$) and ($\angle 2$ and $\angle 4$). We are adding these equal quantities together ($\angle 1 + \angle 2$ and $\angle 3 + \angle 4$).
According to Euclid’s Second Axiom (Common Notion 2), "If equals be added to equals, the wholes are equal."
Since $\angle 1 = \angle 3$ and $\angle 2 = \angle 4$, adding the left sides and the right sides of these equalities respectively, we get:
$\angle 1 + \angle 2 = \angle 3 + \angle 4$
Substituting the expressions for $\angle A$ and $\angle C$:
$\angle A = \angle C$
Thus, we have shown that $\angle A = \angle C$ using Euclid's Second Axiom.
Question 9. In the Fig. 5.9, we have ∠ABC = ∠ACB, ∠3 = ∠4. Show that ∠1 = ∠2.

Answer:
Given:
In the figure provided:
$\angle ABC = \angle ACB$
... (i)
$\angle 3 = \angle 4$
... (ii)
To Prove:
We need to show that $\angle 1 = \angle 2$.
Proof:
From the figure, we can observe the composition of the larger angles:
$\angle ABC$ is the sum of $\angle 1$ and $\angle 4$.
$\angle ABC = \angle 1 + \angle 4$
Similarly, $\angle ACB$ is the sum of $\angle 2$ and $\angle 3$.
$\angle ACB = \angle 2 + \angle 3$
From the given information in equation (i), we know that $\angle ABC = \angle ACB$.
Therefore, we can write:
$\angle 1 + \angle 4 = \angle 2 + \angle 3$
... (iii)
We are also given from equation (ii) that $\angle 3 = \angle 4$.
Substituting $\angle 4$ for $\angle 3$ in equation (iii), we get:
$\angle 1 + \angle 4 = \angle 2 + \angle 4$
According to Euclid's third axiom, "If equals are subtracted from equals, the remainders are equal."
Subtracting $\angle 4$ from both sides of the equation, we get:
$\angle 1 + \angle 4 - \angle 4 = \angle 2 + \angle 4 - \angle 4$
$\angle 1 = \angle 2$
Hence, it is proved that $\angle 1 = \angle 2$.
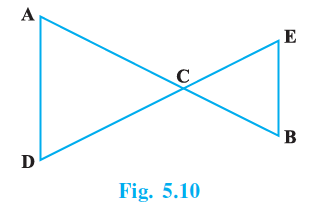
Question 10. In the Fig. 5.10, we have AC = DC, CB = CE. Show that AB = DE.
Answer:
Given:
$AC = DC$
$CB = CE$
To Show:
$AB = DE$
Solution:
From the figure, the length of the line segment AB is the sum of the lengths of the segments AC and CB.
$AB = AC + CB$
Similarly, the length of the line segment DE is the sum of the lengths of the segments DC and CE.
$DE = DC + CE$
We are given that $AC = DC$ and $CB = CE$.
We have two equalities:
$AC = DC$
$CB = CE$
According to Euclid’s Second Axiom (Common Notion 2), "If equals be added to equals, the wholes are equal."
Since AC and DC are equal, and CB and CE are equal, adding AC to CB is the same as adding DC to CE. The sums must be equal.
Adding the corresponding sides of the two given equalities:
$AC + CB = DC + CE$
By substitution, since $AB = AC + CB$ and $DE = DC + CE$, we get:
$AB = DE$
Thus, we have shown that $AB = DE$ using Euclid's Second Axiom.
Question 11. In the Fig. 5.11, if OX = $\frac{1}{2}$ XY, PX = $\frac{1}{2}$ XZ and OX = PX, show that XY = XZ.
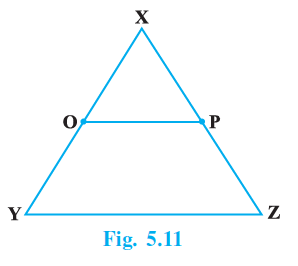
Answer:
Given:
$OX = \frac{1}{2} XY$
$PX = \frac{1}{2} XZ$
$OX = PX$
To Show:
$XY = XZ$
Solution:
We are given the equality:
OX = PX
... (i)
We are also given the relationships:
OX = $\frac{1}{2}$ XY
... (ii)
PX = $\frac{1}{2}$ XZ
... (iii)
From equations (ii) and (iii), we can express XY and XZ in terms of OX and PX respectively by multiplying by 2:
Multiplying (ii) by 2:
$2 \times OX = 2 \times \frac{1}{2} XY$
$2 \times OX = XY$
XY = 2 $\times$ OX
... (iv)
Multiplying (iii) by 2:
$2 \times PX = 2 \times \frac{1}{2} XZ$
$2 \times PX = XZ$
XZ = 2 $\times$ PX
... (v)
Now, we have the equality $OX = PX$ from (i).
According to Euclid's axiom related to multiplication or doubles (implicitly derived from Common Notion 2 or 6), "Doubles of equals are equal".
Since $OX$ and $PX$ are equal quantities, multiplying both by 2 will result in equal quantities.
$2 \times OX = 2 \times PX$
Now, using the results from (iv) and (v), we can substitute XY for $2 \times OX$ and XZ for $2 \times PX$.
$XY = XZ$
Thus, we have shown that $XY = XZ$. The axiom used is that doubles of equals are equal, which is a consequence of Euclid's Second Axiom. Alternatively, one could use Euclid's First Axiom: since $XY$ is equal to $2 \times OX$ and $XZ$ is equal to $2 \times PX$, and $OX = PX$, then $2 \times OX = 2 \times PX$. Since $XY$ and $XZ$ are both equal to quantities which are themselves equal ($2 \times OX$ and $2 \times PX$), then $XY = XZ$.
Question 12. In the Fig.5.12 :

(i) AB = BC, M is the mid-point of AB and N is the mid- point of BC. Show that AM = NC.
(ii) BM = BN, M is the mid-point of AB and N is the mid-point of BC. Show that AB = BC.
Answer:
Part (i):
Given:
$AB = BC$
M is the mid-point of AB
N is the mid-point of BC
To Show:
$AM = NC$
Solution:
Since M is the mid-point of AB, the length of AM is half the length of AB.
$AM = \frac{1}{2} AB$
Since N is the mid-point of BC, the length of NC is half the length of BC.
$NC = \frac{1}{2} BC$
We are given that $AB = BC$.
According to Euclid’s Sixth Axiom (Common Notion 6), "Things which are halves of the same things are equal to one another" or "Halves of equals are equal".
Since AB and BC are equal quantities, their halves must also be equal.
Therefore, $\frac{1}{2} AB = \frac{1}{2} BC$.
By substitution, since $AM = \frac{1}{2} AB$ and $NC = \frac{1}{2} BC$, we have $AM = NC$.
Part (ii):
Given:
$BM = BN$
M is the mid-point of AB
N is the mid-point of BC
To Show:
$AB = BC$
Solution:
Since M is the mid-point of AB, the length of AB is twice the length of BM.
$AB = 2 \times BM$
Since N is the mid-point of BC, the length of BC is twice the length of BN.
$BC = 2 \times BN$
We are given that $BM = BN$.
According to a Euclidean axiom which follows from Common Notion 2, "Doubles of equals are equal".
Since BM and BN are equal quantities, multiplying both by 2 will result in equal quantities.
Therefore, $2 \times BM = 2 \times BN$.
By substitution, since $AB = 2 \times BM$ and $BC = 2 \times BN$, we have $AB = BC$.
Sample Question 1 (Before Exercise 5.4)
Sample Question 1: Read the following statement:
“A square is a polygon made up of four line segments, out of which, length of three line segments are equal to the length of fourth one and all its angles are right angles”.
Define the terms used in this definition which you feel necessary. Are there any undefined terms in this? Can you justify that all angles and sides of a square are equal?
Answer:
The given statement is: “A square is a polygon made up of four line segments, out of which, length of three line segments are equal to the length of fourth one and all its angles are right angles”.
Necessary Definitions of Terms Used:
The terms that need to be defined for a clear understanding of the statement are:
Polygon: A polygon is a closed two-dimensional figure made up of a finite number of straight line segments connected to form a closed chain or circuit.
Line Segment: A line segment is a part of a line that is bounded by two distinct end points, and contains every point on the line between its endpoints.
Angle: An angle is the figure formed by two rays, called the sides of the angle, sharing a common endpoint, called the vertex of the angle.
Right Angle: A right angle is an angle that measures exactly $90^\circ$. It corresponds to a quarter of a full turn.
Length: In this context, length refers to the measure of the distance between the two endpoints of a line segment.
Undefined Terms:
Yes, there are undefined terms in this definition. In Euclidean geometry, the most fundamental concepts are accepted without definition. The terms used in the statement that rely on these undefined concepts are:
Point: A point is considered an undefined term. Euclid described it as "that which has no part," but this is an intuitive description, not a formal definition.
Line: A line is also an undefined term. The definition of a "line segment" relies on the prior concept of a "line."
Plane: Although not explicitly mentioned, figures like polygons exist within a plane, which is another undefined term in geometry.
These terms are foundational, and their properties are established through axioms and postulates rather than definitions.
Justification that all angles and sides of a square are equal:
Given:
From the provided definition of a square, we have:
1. It is a polygon with four line segments. Let the lengths of these segments be $s_1, s_2, s_3,$ and $s_4$.
2. The length of three line segments are equal to the length of the fourth one. We can write this as:
$s_1 = s_4$
$s_2 = s_4$
$s_3 = s_4$
3. All its angles are right angles.
To Justify:
1. All four sides are equal (i.e., $s_1 = s_2 = s_3 = s_4$).
2. All four angles are equal.
Justification:
1. Equality of Sides:
We are given that $s_1 = s_4$, $s_2 = s_4$, and $s_3 = s_4$.
According to Euclid's first axiom, "Things which are equal to the same thing are also equal to one another."
Since $s_1, s_2,$ and $s_3$ are all equal to the same quantity, $s_4$, they must be equal to each other.
Therefore, we can conclude that $s_1 = s_2 = s_3 = s_4$.
This justifies that all four sides of the square are equal.
2. Equality of Angles:
The definition explicitly states that "all its angles are right angles."
A right angle is a specific, constant measure ($90^\circ$).
Since all four angles are right angles, they all have the same measure ($90^\circ$).
Therefore, all four angles of the square are equal.
Exercise 5.4
Question 1. Read the following statement :
An equilateral triangle is a polygon made up of three line segments out of which two line segments are equal to the third one and all its angles are 60° each.
Define the terms used in this definition which you feel necessary. Are there any undefined terms in this? Can you justify that all sides and all angles are equal in a equilateral triangle.
Answer:
The given statement is: “An equilateral triangle is a polygon made up of three line segments out of which two line segments are equal to the third one and all its angles are 60° each.”
Necessary Definitions of Terms Used:
The key terms in this statement that require definition for full comprehension are:
Polygon: A polygon is a closed figure on a plane formed by connecting a finite number of straight line segments end-to-end.
Triangle: A triangle is a polygon with exactly three sides (line segments) and three angles.
Line Segment: A line segment is a portion of a straight line that is bounded by two distinct endpoints and contains every point on the line between its endpoints.
Angle: An angle is formed when two rays (or lines) meet at a common endpoint, called the vertex. The size of the angle is a measure of rotation from one ray to the other.
Degree ($^\circ$): A degree is a unit of measurement for angles. A full circle is divided into 360 degrees. An angle of $60^\circ$ represents $\frac{60}{360}$ or $\frac{1}{6}$ of a full rotation.
Undefined Terms:
Yes, the definition relies on fundamental concepts of geometry that are considered "undefined terms." These terms are accepted intuitively without formal definition, and their properties are described by axioms.
Point: A point specifies a location but has no dimension (no length, width, or depth). It is the most basic object in geometry. The ends of a line segment are points, and the vertex of an angle is a point.
Line: A line is a straight, one-dimensional figure that extends infinitely in both directions. The term "line segment" is defined as a part of a line.
Plane: A plane is a flat, two-dimensional surface that extends infinitely. A polygon, such as a triangle, is a figure that lies on a plane.
Justification that all sides and all angles are equal:
The justification can be derived directly from the provided statement using logical reasoning and Euclid's axioms.
1. Justification of Equal Sides:
The statement says the triangle is "made up of three line segments out of which two line segments are equal to the third one."
Let the lengths of the three line segments (sides) be $l_1, l_2,$ and $l_3$.
From the statement, we can interpret this as:
$l_1 = l_3$
$l_2 = l_3$
According to Euclid's first axiom, "Things which are equal to the same thing are also equal to one another."
Since both $l_1$ and $l_2$ are equal to the same length $l_3$, they must be equal to each other. So, $l_1 = l_2$.
Combining these equalities, we get $l_1 = l_2 = l_3$.
Thus, all three sides of the equilateral triangle are equal.
2. Justification of Equal Angles:
The statement explicitly says that "all its angles are 60° each."
Let the three angles be $\angle A, \angle B,$ and $\angle C$.
According to the statement:
$\angle A = 60^\circ$
$\angle B = 60^\circ$
$\angle C = 60^\circ$
Since all three angles are specified to have the same measure ($60^\circ$), they are, by definition, equal to one another.
Thus, all three angles of the equilateral triangle are equal.
Question 2. Study the following statement:
“Two intersecting lines cannot be perpendicular to the same line”. Check whether it is an equivalent version to the Euclid’s fifth postulate.
[Hint: Identify the two intersecting lines l and m and the line n in the above statement.]
Answer:
Understanding the Task:
The task is to determine if the statement, “Two intersecting lines cannot be perpendicular to the same line,” is an equivalent version of Euclid’s fifth postulate. To do this, we need to show that the statement can be logically derived from the fifth postulate, and conversely, that the fifth postulate can be derived from the statement.
Euclid’s Fifth Postulate and its Equivalent:
Euclid's fifth postulate is famously complex. A more modern and commonly used equivalent version is Playfair's Axiom, which states:
“For a given line and a point not on the line, there is exactly one line through the point parallel to the given line.”
We will use Playfair's Axiom to check for equivalence.
Analysis of the Given Statement:
Let's break down the given statement: “Two intersecting lines cannot be perpendicular to the same line”.
Let's call this statement (S1).
Consider two lines, $l$ and $m$, that intersect at a point $P$. Let $n$ be another line. The statement (S1) asserts that it is impossible for both $l \perp n$ and $m \perp n$ to be true simultaneously.
We will check for equivalence by showing that (S1) is logically equivalent to Playfair's Axiom.
Proof of Equivalence:
Part 1: Proving that Playfair's Axiom implies the statement (S1).
We assume Playfair's Axiom is true and try to prove (S1).
Let $l$ and $m$ be two lines that intersect at point $P$. We will use proof by contradiction. Let's assume that it is possible for these intersecting lines to be perpendicular to the same line, $n$.
Assume $l \perp n$ and $m \perp n$.
A standard theorem in Euclidean geometry (which relies on the fifth postulate) states that if two lines are perpendicular to the same line, then they are parallel to each other. Therefore, since both $l$ and $m$ are perpendicular to $n$, it must be that $l \parallel m$.
However, this contradicts our initial condition that lines $l$ and $m$ intersect at point $P$. Since our assumption leads to a contradiction, the assumption must be false.
Therefore, two intersecting lines cannot be perpendicular to the same line. This shows that Playfair's Axiom implies statement (S1).
Part 2: Proving that the statement (S1) implies Playfair's Axiom.
Now, we assume the statement (S1) is true and try to prove Playfair's Axiom.
Playfair's Axiom has two parts: the existence of a parallel line and the uniqueness of that line. The existence can be proven without the fifth postulate, so the crucial part is to prove uniqueness.
Uniqueness Proof: Let $L$ be a line and $P$ be a point not on $L$. We want to prove there is at most one line through $P$ that is parallel to $L$.
Let's construct a line $t$ through $P$ such that $t \perp L$. Let the intersection point be $Q$.
Now, let's construct a line $M$ through $P$ such that $M \perp t$.
We will now use proof by contradiction. Assume there is another line, $N$, also passing through $P$, which is parallel to $L$, and $N$ is distinct from $M$.
Since $L \parallel N$ (by assumption), and line $t$ is perpendicular to $L$, it must be that line $t$ is also perpendicular to $N$. (A line perpendicular to one of two parallel lines is perpendicular to the other).
So now we have:
- Line $M$ passes through $P$ and $M \perp t$.
- Line $N$ passes through $P$ and $N \perp t$.
This means we have two lines, $M$ and $N$, both intersecting at point $P$ and both perpendicular to the same line $t$.
This situation directly contradicts our initial assumption, the statement (S1): “Two intersecting lines cannot be perpendicular to the same line”.
Since our assumption (that a second parallel line $N$ exists) leads to a contradiction, the assumption must be false. Therefore, there can be only one line through $P$ parallel to $L$. This proves the uniqueness part of Playfair's Axiom.
Conclusion:
We have shown that:
1. Euclid's fifth postulate (in the form of Playfair's Axiom) implies the given statement.
2. The given statement implies Euclid's fifth postulate (Playfair's Axiom).
Since the two statements are logically derivable from each other, they are equivalent.
Yes, the statement “Two intersecting lines cannot be perpendicular to the same line” is an equivalent version of Euclid’s fifth postulate.
Question 3. Read the following statements which are taken as axioms :
(i) If a transversal intersects two parallel lines, then corresponding angles are not necessarily equal.
(ii) If a transversal intersect two parallel lines, then alternate interior angles are equal.
Is this system of axioms consistent? Justify your answer.
Answer:
Understanding the Question:
We are given two statements that are to be treated as axioms. We need to determine if this system of axioms is "consistent". A system of axioms is considered consistent if it does not lead to any contradictions. In other words, it should be impossible to prove a statement and its opposite (negation) from the same set of axioms.
The Given Axioms:
Axiom (i): If a transversal intersects two parallel lines, then corresponding angles are not necessarily equal.
Axiom (ii): If a transversal intersects two parallel lines, then alternate interior angles are equal.
Analysis and Justification:
Let's see if these two axioms can coexist without creating a contradiction. We will start with Axiom (ii) and use it, along with other basic geometric principles, to see what it implies about corresponding angles.
Consider two parallel lines, $l$ and $m$, intersected by a transversal line $t$.
In the figure:
- $\angle 3$ and $\angle 5$ are a pair of alternate interior angles.
- $\angle 1$ and $\angle 5$ are a pair of corresponding angles.
- $\angle 1$ and $\angle 3$ are a pair of vertically opposite angles.
Let's proceed with a logical deduction:
1. According to Axiom (ii), since lines $l$ and $m$ are parallel, the alternate interior angles are equal.
$\angle 3 = \angle 5$
... (a)
2. We know from a fundamental theorem of geometry (which does not depend on the parallel postulate) that vertically opposite angles are equal.
$\angle 1 = \angle 3$
[Vertically Opposite Angles] ... (b)
3. Now, we use Euclid's first axiom ("Things which are equal to the same thing are also equal to one another"). From equations (a) and (b), since both $\angle 1$ and $\angle 5$ are equal to $\angle 3$, they must be equal to each other.
$\angle 1 = \angle 5$
This means that we have logically proved from Axiom (ii) that "If a transversal intersects two parallel lines, then corresponding angles are equal."
Checking for Consistency:
Let's compare our finding with Axiom (i).
- Result derived from Axiom (ii): Corresponding angles are equal.
- Statement from Axiom (i): Corresponding angles are not necessarily equal.
These two statements are direct contradictions of each other. The system requires us to accept both that corresponding angles are equal and that they are not necessarily equal. This is a logical impossibility.
Conclusion:
The system of axioms is not consistent. It is inconsistent because Axiom (ii), when combined with the basic theorem about vertically opposite angles, leads to a conclusion that is the direct opposite of Axiom (i). A consistent system cannot contain an axiom and also allow for the proof of that axiom's negation.
Question 4. Read the following two statements which are taken as axioms :
(i) If two lines intersect each other, then the vertically opposite angles are not equal.
(ii) If a ray stands on a line, then the sum of two adjacent angles so formed is equal to 180°.
Is this system of axioms consistent? Justify your answer.
Answer:
Understanding the Question:
We are given a system of two statements that are to be treated as axioms. The task is to determine if this system is "consistent". A system of axioms is consistent if it does not lead to a logical contradiction. That is, we should not be able to prove a statement that is the opposite of another statement within the system.
The Given Axioms:
Axiom (i): If two lines intersect each other, then the vertically opposite angles are not equal.
Axiom (ii): If a ray stands on a line, then the sum of two adjacent angles so formed is equal to 180°.
Analysis and Justification:
To check for consistency, we will use Axiom (ii) and basic logic to see what conclusion it leads to regarding vertically opposite angles. We will then compare this conclusion with Axiom (i).
Let two lines, which we can call $AB$ and $CD$, intersect at a point $O$.
This intersection creates pairs of vertically opposite angles ($\angle AOC$ and $\angle BOD$; $\angle AOD$ and $\angle BOC$) and pairs of adjacent angles that form a linear pair.
Now, let's apply Axiom (ii), which is also known as the Linear Pair Axiom.
1. Consider the ray $OC$ standing on the line $AB$. According to Axiom (ii), the sum of the adjacent angles is 180°.
$\angle AOC + \angle BOC = 180^\circ$
... (a)
2. Now, consider the ray $OB$ standing on the line $CD$. Again, according to Axiom (ii), the sum of these adjacent angles is 180°.
$\angle BOC + \angle BOD = 180^\circ$
... (b)
3. From equations (a) and (b), we can see that both expressions equal 180°. Using the axiom that "Things which are equal to the same thing are also equal to one another", we can set the left sides of the equations equal to each other.
$\angle AOC + \angle BOC = \angle BOC + \angle BOD$
4. Now, we use the axiom that "If equals are subtracted from equals, the remainders are equal". We subtract $\angle BOC$ from both sides of the equation.
$\angle AOC + \angle BOC - \angle BOC = \angle BOC + \angle BOD - \angle BOC$
$\angle AOC = \angle BOD$
The angles $\angle AOC$ and $\angle BOD$ are a pair of vertically opposite angles. Our logical deduction from Axiom (ii) shows that they are equal.
Checking for Consistency:
Let's compare our derived result with Axiom (i).
- Result derived from Axiom (ii): Vertically opposite angles are equal.
- Statement from Axiom (i): Vertically opposite angles are not equal.
These two statements are direct contradictions. The system of axioms simultaneously asserts that vertically opposite angles are not equal (Axiom i) and implies that they are equal (a consequence of Axiom ii). A logical system cannot hold two contradictory statements to be true at the same time.
Conclusion:
The system of axioms is not consistent. It is inconsistent because Axiom (ii) logically leads to a conclusion that is the direct negation of Axiom (i).
Question 5. Read the following axioms:
(i) Things which are equal to the same thing are equal to one another.
(ii) If equals are added to equals, the wholes are equal.
(iii) Things which are double of the same thing are equal to one another.
Check whether the given system of axioms is consistent or inconsistent.
Answer:
Understanding the Question:
We are given a system of three statements, treated as axioms. We need to check if this system is consistent. A system of axioms is considered consistent if its axioms do not contradict each other. In other words, it should not be possible to use one axiom to prove a statement that is the opposite of another axiom.
The Given Axioms:
Axiom (i): Things which are equal to the same thing are equal to one another.
This is Euclid's first common notion, also known as the transitive property of equality. If $a=c$ and $b=c$, then $a=b$.
Axiom (ii): If equals are added to equals, the wholes are equal.
This is Euclid's second common notion, the addition property of equality. If $a=b$ and $c=d$, then $a+c = b+d$.
Axiom (iii): Things which are double of the same thing are equal to one another.
If $a = 2c$ and $b = 2c$, then $a=b$.
Analysis and Justification:
To check for consistency, let's examine the relationship between these axioms. Let's see if Axiom (iii) can be derived from the other axioms. If it can, it means it is a logical consequence of them and cannot contradict them.
Let's start with the premise of Axiom (iii).
Suppose we have two things, $x$ and $y$, which are "double of the same thing", say $z$.
Mathematically, this means:
$x = 2z$
$y = 2z$
Now, let's apply Axiom (i): "Things which are equal to the same thing are equal to one another."
In our case:
- The thing $x$ is equal to $2z$.
- The thing $y$ is equal to the same thing, $2z$.
Since both $x$ and $y$ are equal to the same thing ($2z$), according to Axiom (i), they must be equal to one another.
Therefore, we can conclude that $x=y$.
This is exactly what Axiom (iii) states. This means that Axiom (iii) is not an independent axiom but is actually a special case or a direct logical consequence of Axiom (i).
Conclusion:
The system of axioms is consistent.
The justification is that Axiom (iii) is not a new, independent rule that could potentially contradict the others. Instead, it is a result that can be proven using Axiom (i). A statement that is a logical consequence of an axiom cannot contradict that axiom. All three statements are fundamental truths about the concept of equality and do not conflict with one another in any way.

